
Data Analysis
Unit Pre-Test and Post-test
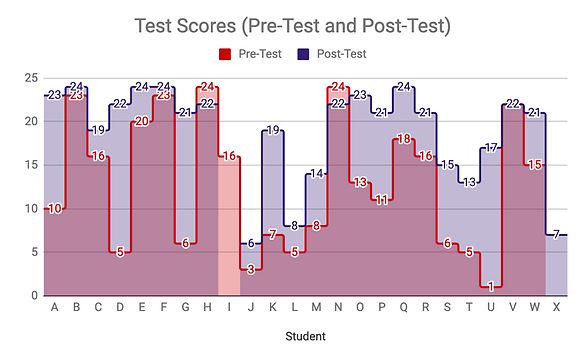
Prior to students being exposed to any of the lessons in our fifth math unit, students were given a pre-test that was very similar to the layout of their final unit test. Both tests were scored out of 24 points. As noted in my rationale, at the time of the pre-test, I had 26 students in my classroom. However, 2 students are not included in the data described over the course of this data analysis due to parent request. Additionally, student I does not have any post-test data because she moved before she had the opportunity to take it. As shown on the first graph, the initial scores, found in red, varied greatly. Some students scored as low as 1 or 3 points out of 24 whereas others received a perfect score or a near perfect score. In addition to the variance in student scores, student X did not take the pre-test because they were absent the day that pre-test was given. The post-test, highlighted in purple, demonstrates the growth that the majority of students made between their pre-test and post-test scores. Only two students decreased in their scores, and these were the students that received perfect scores the first time. Student V received the same score on both the pre and post-test.
Ultimately the data suggests that the majority of students made growth in their math achievement based on my implementation of differentiated math instruction. However, some students made less growth than their peers. For example, students J and L grew 3 points. These particular students were part of the intervention group that met with me throughout the week and with paraprofessionals on days that I met with other groups of students. Therefore, both students spent a lot of time with teachers, but still made less growth than what was expected. This suggested that despite the unit concluding, these students required further reteaching to access the content and reach grade-level expectations Both students needed more individualized support as opposed to receiving instruction in a small group; the group may have moved too quickly for them.
Student M was a student who typically does not struggle with math; however, she also showed less growth than expected. In addition to the snow days that we had throughout the implementation of this unit of math, she was absent for a week of school and missed a lot of instruction. Therefore, she might have benefited from reteaching as well.
While analyzing the data further, I found that some of my students who received high scores the first time did not make as much growth. More specifically, students H and N dropped two points. When looking at their post-test, I found that they made small mistakes which suggested that they were going too fast. For example, student H had demonstrated his ability to write his numbers past 1000 in the past; however, on his test, he skipped from 100 to 111 instead of 101. Student V was also one who showed no growth based on the post-test. These three students were in my small group where we practiced multi-step problems rather than reviewing standard content, like the other groups. Therefore, the data suggested that it may have been beneficial to review with these students as well, not just the students in the high average, average, and below average small groups.
Although students who did not make significant progress have been described, there were also some students who demonstrated a lot of growth between their pre-test and post-test data. For example, student U only received 1 point the first time he took this test and received 17 out of 24 points the second time. This is also a student who expressed a lot of frustration with math in the past and was in my intervention small group. As a result, the data suggested that additional time with the paraprofessionals and myself benefited him. Students D and G also made significant progress after scoring fairly low the first time. In addition, students O, P, Q, and R scored fairly well the first time and received scores in the 20’s the second time.
Quick Quizzes

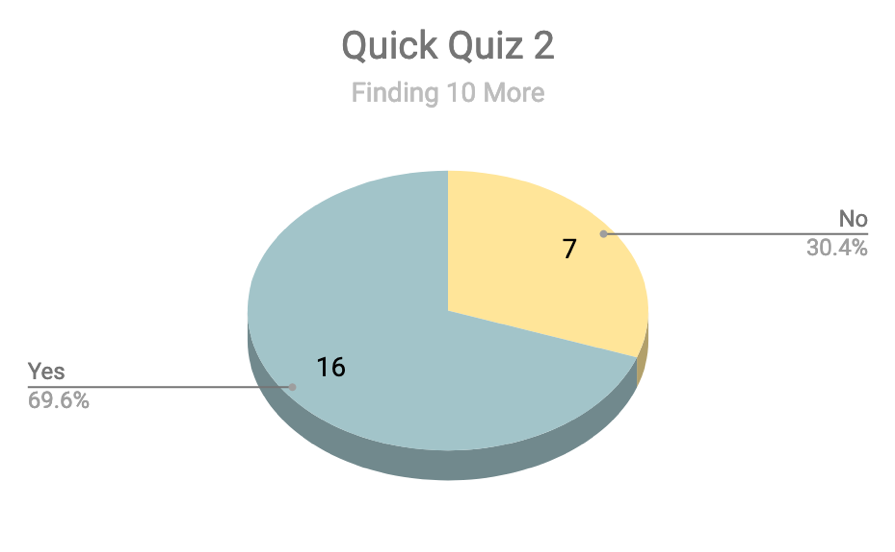
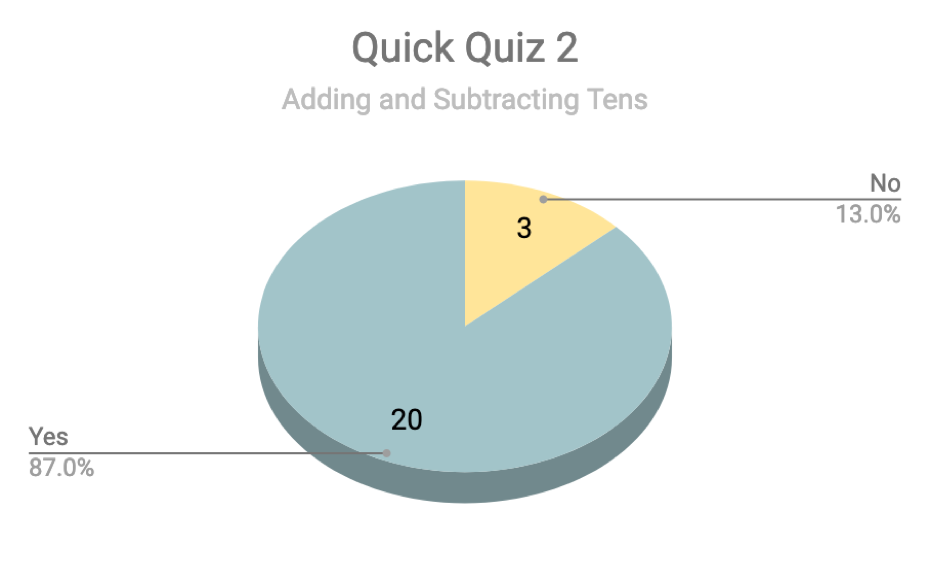

As can be seen from the graphs, a variety of skills were assessed on the second quick quiz whereas the first quick quiz solely focused on finding unknowns in addition and subtraction problems within 20. Therefore, I broke down the second quick quiz into the different skills covered due to the fact that some concepts such as finding 10 more than a given two-digit number were more difficult than other skills for some students. As can be seen, the total number of students assessed was different between both quick quizzes. On the first quiz, one student was not included in the data due to the fact that he received special education services and received help with math. This is the same student previously noted in the pre-test and post-test data over the unit test. This student was also not included on the second quick quiz. In addition, a student that missed a week of school was not included in the second quick quiz data. However, it can be assumed that because she was absent for a lot of the content covered that she would not have demonstrated proficiency with these skills. Although only five students were not able to demonstrate that they were able to find a rule in a number pattern and continue it, it was a skill we continued to practice and review as a class, especially because one question does not necessarily demonstrate mastery. Additionally, on their work pages over number patterns, some of my higher ability students noted how hard it was. We also continued to review 10 more and 10 less than a number due to the fact that this was within the learning continuum for many of my students based on MAP data collected in the winter. Furthermore, adding and subtracting was a skill that continued to be reviewed up until the test due to the fact that their quiz only had two questions pertaining to this skill whereas the test had six questions over this skill. The ability to add and subtract multiples of ten also sets the foundation for adding and subtracting double-digit numbers.
Student Interviews
In order to assess my students’ perceptions and attitudes regarding mathematics as well as their prior knowledge, I began the unit by interviewing a small sample of students of varying ability levels. This provided me the opportunity to assess whether my students who typically struggled with math did not like it due to the frustration it may have brought and if my high ability students found math boring. Furthermore, students who were on-level may not always have their voices heard as much as the high ability students and the students that struggle because these are the students we tend to focus on in order to differentiate learning experiences. Six students were interviewed, four boys and two girls, at the beginning of the unit and at the end of the unit. The data from the initial interviews suggested that all six students had mostly positive attitudes toward math. When asked if they liked it, five students responded with a yes that they liked math. The only outlier was a student who stated that she felt “so-so” because she liked reading better. A different student responded that he liked it better than reading because it was harder and because it was more fun. Additionally, three students noted that they like math because it helped them learn. Other responses included that students enjoyed addition and subtraction. The second question that students were asked was what their favorite thing about math so far in the year. Four out of six students mentioned they liked addition. One mentioned he liked subtraction because it is harder than addition. Another participant mentioned she liked multiplication because she is learning it at home with her sister.
After asking students a couple of questions about math in general, to gain an understanding of attitudes toward math, the other two questions allowed me to see if students had any prior knowledge before being exposed to content. As already noted, the first question involved three addends. 4 and 6 were two of the addends because I wanted to see if students were already familiar with the make-a-ten strategy. Once asked this question, two students said they did not know how to solve it. A couple of other students said they would use tallies or sticks and circles. The last two students mentioned they would add 8 and then combine the 4 and 6. Therefore, as a result of this interview, I was able to see that two students already had some prior knowledge and may not need as much practice as others. The final question asked students to add a two-digit number and a multiple of ten. Two of the six students stated that they did not know. One student stated she would use tallies because it was faster to count by 5’s and another said he would draw dots. The last two students were able to find the answer correctly. One knew to draw ten sticks and circles to help her solve and the other used vertical form; however, he mentioned he would start with the tens so this statement suggests he would benefit from additional practice in order to be more successful with regrouping.
After completing our unit in math, the same six students were interviewed to see if their perceptions and skills had changed over the course of the unit. As seen with the first interviews, five out of six said they liked math and the same student who said she felt “so-so” continued to feel neutral because she continued to like reading better. Two students also re-stated that they liked math because "we learn". One student stated he liked math because it made him “get better and better and better”. This quote suggested that he showed growth over the few weeks due to the fact that his initial response was that he liked easy math like addition and subtraction. Another student who had stated she liked learning later stated that math is full of hard problems and she likes “hard stuff”. The response from this student, in particular, suggests the importance of challenging students while providing encouragement and support. One of the higher level students stated he enjoyed math because there are many different kinds of math. Initially, he had said he liked it because it was harder than reading. Again, students were asked what their favorite part of math was and a couple re-stated they like addition and subtraction; however, one began to add specific examples such as 5+5, 1+1, 2+2, and so on. This suggested he enjoyed working with doubles. Additionally, he stated he liked making circles and sticks. This student was one of my students who tended to struggle more so I was a little surprised by this due to the fact place value had been a point of frustration in the past for him. The student who stated they liked the hard problems also mentioned that she enjoyed learning to subtract and count on so when she grew up she could count money. While planning out this unit, I created a Jeopardy game to review the different skills with students that we covered. One student stated this was his favorite thing about math so far this year because they had the opportunity to choose what kind of question they wanted and how hard it was. In addition, another student mentioned she liked true and false equations. This was not covered much during the unit; however, it was a focus in Jeopardy which suggests this may have been one of her favorite activities.
In regard to seeing how students’ number sense and problem-solving skills grew as a result of the instruction of this unit, the same two questions involving the make-a-ten strategy and double-digit addition were used. Whereas in the first interview a couple of students did not know how to solve the last two questions and did not attempt either of them, all students attempted both questions in the post interview. This led me to believe that their confidence grew, as well as their math skills, over the course of the weeks that we were learning the content covered. Only two students knew to use the make-a-ten strategy at first and four were able to find the tens partners the second time they were interviewed. The two lower performing students were the two that drew dots to solve; however, both showed growth from not knowing where to start. The second question focused on adding multiples of ten. Although the students who did not know still struggled to solve the question correctly, they attempted it without becoming frustrated. The other four students were able to solve for the answer correctly as opposed to just two. In addition, growth was seen from the students who wanted to draw dots or tallies for both numbers to just using tens sticks and circles to be more efficient.
Multi-Step problem solving
(Small Group)

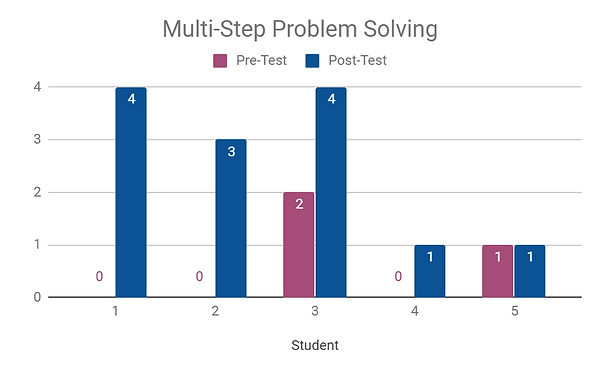
Due to the fact that some students had already mastered the majority of the content to be covered during the unit, I provided an extension during small group instruction for five students as opposed to continuing to reinforce something with which they already had a solid foundation. After analyzing their MAP data and considering what we were learning in class, I focused on providing instruction on multi-step problems with addition and subtraction. Additionally, these double-digit addition and subtraction problems provided students practice with regrouping. The pre-test data showed that the five students ranged in their ability to identify whether or not they needed to add, subtract, or use both operations; however, at the end of instruction, all five students were able to correctly identify the operations to be used for all four problems. In regard to problem-solving, three students were initially unable to solve any of the problems correctly. The other two students were unable to solve all four problems accurately. However, the post-test data demonstrated that four students made growth, while one remained neutral. Therefore, the errors that resulted were based on problem-solving as opposed to operation identification. These students were met with for a total of four times. The first time and fourth time were dedicated to taking the pre-test and post-test. Explicit instruction of multi-step problems was conducted two times during the math unit. Additionally, I planned on this group having time to also practice with rounding to the nearest ten and hundred, but due to snow days, this was unable to occur. This also meant we could not meet twice a week as planned on some weeks.
When comparing the data from both graphs, student 1 made significant growth. Initially, he was unable to correctly identify the operations to be used and solved all four problems incorrectly, but on the post-test was able to solve all four questions correctly in regard to both operation identification and problem-solving. Therefore, this instruction appears to have been very beneficial for extending his learning. Student 2 was able to accurately identify operations for all four problems and made no growth due to to the fact this was a skill he had already acquired. Problem-solving was an area where he initially struggled and only missed one on the post-test. In comparison to the other students, student 3 appeared to be the most familiar with these problems and only incorrectly identified the operations to be used in one of the problems on the pre-test. When it came to problem-solving, he correctly solved two of the problems the first time and was able to correctly solve all four on the post-test. Students 4 and 5 made the least amount of progress in regard to problem-solving. Evidence from their post-tests demonstrated an increased understanding of vertical form but also showed that regrouping was a difficult skill for these students to acquire. Therefore, these two students could benefit from more time working with regrouping problems in isolation to build their foundation prior to solving these equations in multi-step problems. However, as already noted, they were able to correctly identify the operations to be used in all four problems on the post-test. It was also noted that snow days contributed to inconsistency in meeting times with these students. Therefore, in the future, I would work to provide students with more time to practice with me or their other group members to continue strengthening their foundation. It is likely that for students, such as 4 and 5, that the inconsistency in meeting times contributed to more confusion in how to solve problems.
Triangulation of data
The purpose of my action research was to determine if data-driven, differentiated planning during small group mathematics instruction increased student achievement in math. Overall, the post-test data from the unit test demonstrated an increase in the majority of student scores in comparison to the pre-test scores. Furthermore, the data collected from most of the students exposed to solving multi-step problems in the extension group demonstrated an increase in student scores. Therefore, both sets of data as a whole confirm the hypothesis that data-driven differentiated planning during small group mathematics instruction increased student achievement. Although the amount of growth varied per student, an increase in mathematical achievement was what this action research aimed to measure. The use of student interviews enriched my data analysis because I was able to observe how perceptions and problem-solving skills evolved over the course of the study in addition to an overall increase in student scores. A couple of students started the unit by saying they did not know how to solve problems and then were able to at least attempt to solve what was being asked of them. One of the students, who tended to have more difficulty with math and told me that he did not know how to solve the two problems presented in the interview, grew 16 points between his pre-test and post-test data on the unit test. He also stated in the post interview that math helps him “get better and better and better” which suggested that he had a positive outlook on math. In addition to being asked to solve problems, students’ perceptions were analyzed. Analysis of student perceptions generated the common themes that students generally have positive attitudes about math and that their confidence in their ability to answer problems increased further explaining the increase in post-test scores. One of my higher achieving students, who was in the small group that focused on multi-step problems, noted that his favorite thing about math that we had done was the Jeopardy game. He specifically mentioned he liked having the opportunity to choose what they wanted to answer a question about and how hard the question was. This leads me to believe that encouraging student choice truly is a powerful motivator in a classroom environment. Although not all students were interviewed, their knowledge base and confidence in being able to solve problems can be observed based on what is written on their post-test. For example, many students who were not interviewed did not attempt to answer all questions on the pre-test if they did not have an idea of where to begin; however, on the post-test, all questions were answered or attempted by students that took the test. Results from the post-interviews and post-test data, in comparison to the data collected before the unit, suggest that students’ confidence in their ability to solve problems increased.
However, as already noted, when comparing the pre-test and post-test data from the unit test, a couple of student scores decreased and one student received the same score the second time. These three students seemingly refuted my hypothesis based on their unit test data alone and were also in my small group. Their data leads me to believe that they could have benefited from a short review of what we had been learning in class each time we met or a review of the importance of going back to check work once they answer a question. When analyzing this data further, one of the students that received a lower score on the unit post-test made progress in the extension group in regard to both his ability to identify the operations to be applied and accurately solve the story problems presented. Additionally, the data from his unit test suggests that he went through the test too quickly the second time and made small errors. For example, this student was to continue a number pattern three times on the unit test. He wrote the first two numbers in the extended pattern correctly; however, he repeated the second number instead of adding 5 to continue the pattern. When analyzing his quick quiz data, he received perfect scores on both which would further explain his unexpected achievement level on the unit post-test. Ultimately, the data suggests this student increased in his mathematical achievement. Furthermore, the student who remained stagnant on the unit post-test as well as on her multi-step problem-solving quiz mentioned in her interview both times that she felt "so-so" about math due to the fact that she liked reading better. This statement further explains why she may not have made as much progress as her peers as would be expected with the differentiated instruction.
Overall, after analyzing the data collected throughout the unit, the hypothesis that data-driven, differentiated planning during small group mathematics instruction increases student achievement in math is confirmed, even when considering the outliers who seemingly refuted this claim due to a further analysis and explanation of their data.
Student Impact and examination of researcher
interactions and practices
Due to the fact that the majority of students made growth from their pre-test data to their post-test data, the data suggests the impact on students was very positive. Additionally, the small group that I worked with made significant progress, including the two students who continued to have difficulty in problem-solving with regrouping. This could be seen from their responses on the pre-test and their work shown on their pre-test. I believe they liked the challenge due to the fact that one of them asked “can we solve the last one?” when I told them we ran out of time in order to begin unit studies on time. The small sample of students that were interviewed demonstrated that they enjoyed having time to talk with me one-on-one, even if it pertained to academics. Furthermore, hearing that a game we used to review math was one of my students’ favorite parts of math was useful to hear because I will continue looking for games and ways to provide students with choice in mathematics as well as all subject areas.
In my initial action plan, I had intended to cover two separate topics with my extension small group due to the fact that I thought they would pick up on multi-step problem solving fairly quickly. However, as I soon realized, regrouping was a skill they struggled with which impacted their ability to solve these problems. This prior lack of understanding of regrouping caused me to extend the amount of time spent on the concept. Additionally, interruptions from snow days caused an increased need to review what we had previously learned in order to refresh students’ memories. When assessing this group for the first time to collect pre-test data, I gave the test orally, as we tend to do when practicing story problems at the carpet in a whole group setting. This then led to students having to focus on listening skills as well while being exposed to something for the first time which caused frustration. Because I realized this was an ineffective measure of what they already knew, I redid the pre-test for this group so the story problems were already written out on their paper. On some days, I also combined groups in order to review concepts, especially when there were snow days and one group lost their work time with me. This could be another reason why some groups did not receive the more personalized instruction that was intended.
Questions that arose from the Data
Why did some students in the intervention group not make as much progress?
When analyzing the data, I had hoped that my intervention group would make more progress than they did. Students S and U appeared to have benefitted from the additional work time with myself, as well as the two paraprofessionals that we have on Thursdays and Friday, but students J, L, and X did not. However, student X was also gone for multiple days due to illness which is why there was no pre-test data for her. Student J and L could have, potentially, benefited from more individualized instruction if the intervention group, as a whole, moved more quickly than what they were ready for. Additionally, there were a couple of days during this unit in which our Thursday para was not able to assist with classroom activities and one of our snow days this year fell on a Thursday so this group did not receive the anticipated minimum of three days worth of additional instruction.
What concepts needed to be reviewed after the unit was completed?
On the second quick quiz, 7 students struggled to find 10 more than a provided 2-digit number, so this was a concept we came back to and reviewed in order to clarify any misconceptions. On the test, some students continued to have difficulty answering a question involving 10 more and 10 less as well; however, this math problem produced a lot of student questions and confusion due to the fact that there were 4 steps required in order to successfully address what was being asked. This was something that we practiced as a whole group when we played Jeopardy, but due to the fact that they answered in groups, it may have not been as beneficial. In the future, if I were to play Jeopardy again and use this as a final Jeopardy question, I would have each group member answer as an exit ticket.




